对于刚加入我们的人……
AV1 是一种由 开放媒体联盟 开发的新通用视频编解码器。该联盟开始使用 Google 的 VPX 编解码器、Cisco 的 Thor 编解码器以及 Mozilla/Xiph.Org 的 Daala 编解码器作为起点来开发新的编解码器。AV1 实现了超越 VP9 和 HEVC 的性能，使其成为下一代编解码器亮度预测中的色度 功能。今天，我们将介绍受限方向增强滤波器。如果您一直想知道编解码器的编写过程，请系好安全带，准备学习！

AV1 中的滤波

几乎所有视频编解码器都使用增强滤波器来提高主观输出质量。

我所说的“增强滤波器”是指不一定编码图像信息或提高客观编码效率，但以某种方式使输出看起来更好的技术。必须谨慎使用增强滤波器，因为它们往往会丢失一些信息，因此有时会被视为一种欺骗性的作弊手段，用来使输出质量看起来比实际更好。

但这不公平。增强滤波器旨在减轻或消除客观指标无法识别但人眼却能明显察觉到的特定伪影。即使滤波是一种作弊形式，一个好的视频编解码器也需要它能够部署的所有实用且有效的作弊手段。

滤波器分为多个类别。首先，滤波器可以是规范性的或非规范性的。规范性滤波器是编解码器的必要组成部分；如果没有它，就不可能正确解码视频。非规范性滤波器是可选的。

其次，滤波器根据其应用位置进行划分。有预处理滤波器，在编码开始前应用于输入；后处理滤波器，在解码完成后应用于输出；以及环内或仅环路滤波器，它们是编码循环中编码过程的组成部分。预处理和后处理滤波器通常是非规范性的，并且位于编解码器的外部。环路滤波器几乎在定义上就是规范性的，并且是编解码器本身的一部分；它们用于编码优化过程中，并应用于存储的参考帧或帧间编码。

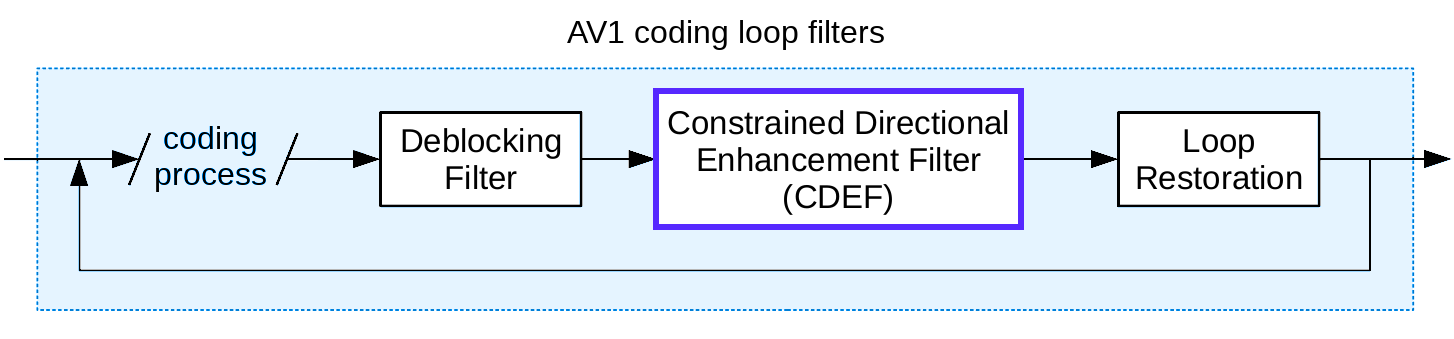AV1 在编码循环中使用三个规范性增强滤波器。第一个是去块滤波器，顾名思义，它消除了编码块边缘明显的边界伪影。虽然 DCT 相对比较适合压缩自然图像中的能量，但它仍然倾向于将误差集中在块边缘。请记住，消除这种块效应是 Daala 使用重叠变换的主要原因，但是 AV1 是一种更传统的编解码器，具有硬块边缘。因此，它需要传统的去块滤波器来平滑块边缘伪影。

传统 DCT 块基编解码器中的块效应示例。块边缘的误差特别明显，因为它们形成了硬边缘。更糟糕的是，DCT（以及 DCT 系列中的其他变换）倾向于将误差集中在块边缘，从而加剧了问题。

最后三个滤波器中的一个是环路恢复滤波器。它由两个可配置和可切换的滤波器组成，一个 维纳滤波器 和一个 自引导 滤波器。两者都是卷积滤波器，试图构建一个内核来恢复原始输入图像的一些丢失的质量，通常用于降噪和/或边缘增强。对于 AV1 的目的，它们实际上是通用降噪滤波器，通过可配置量的模糊来去除 DCT 基噪声。

这两个滤波器之间的滤波器，即受限方向增强滤波器 (CDEF) 是我们这里感兴趣的；与环路恢复滤波器一样，它消除了锐利边缘周围的振铃和基噪声，但与环路恢复滤波器不同，它是方向性的。它可以跟随边缘，而不是像大多数滤波器那样盲目地向所有方向滤波。这使得 CDEF 尤其有趣；它是视频编码中应用的第一个实用且有用的方向性滤波器。

漫长而曲折的道路

CDEF 的故事并不完全是线性的；它漫长而充满回溯、旁枝和死胡同。CDEF 将多条研究路径融合在一起，每条路径都为最终的 AV1 中的受限方向增强滤波器提供了一个想法或灵感。“方向性”方面是 CDEF 在实现上特别新颖的地方，但也借鉴了几个不同地方的想法和灵感。

使用 DCT 和类似 DCT 的变换变换像素数据块的全部目的是使用更少的数字来表示该像素数据块。DCT 非常擅长压缩大多数视觉图像中的能量，也就是说，它倾向于将分散的像素模式收集到少数几个重要的输出系数中。

DCT 的压缩效率存在例外。举两个最常见的例子，DCT 无法很好地表示方向边缘或模式。如果我们绘制锐利对角线边缘的 DCT 输出，我们会发现输出系数也形成了……一个锐利的对角线边缘！边缘在变换后有所不同，但它仍然存在，并且通常比开始时更复杂。压缩失败！

尖锐特征是基于 DCT 的编解码器的传统问题，因为它们无法很好地压缩，即使根本无法压缩。在这里，我们看到一个锐利边缘（左）及其 DCT 变换系数（右）。原始边缘的能量以方向性波纹模式散布在 DCT 输出中。

在过去的二十年中，视频编解码器研究越来越多地关注本质上是方向性的变换、滤波器和预测方法，以此作为更好地表示方向边缘和模式以及纠正 DCT 的这一基本局限性的方法。

经典的方向预测器

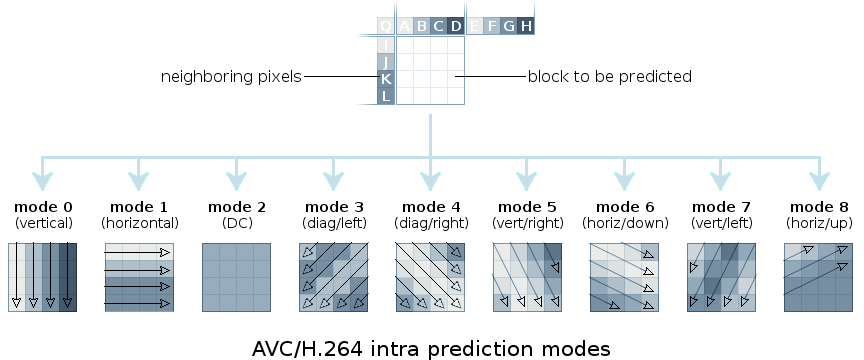
方向性帧内预测可能是现代视频编解码器中使用最广为人知的方向性技术之一。我们都熟悉 h.264 和 VP9 的方向性预测模式，其中编解码器根据已解码块的周围像素模式预测新块中的方向性模式。目标是在变换块之前消除（或大幅减少）硬方向边缘中包含的能量。通过预测和去除无法压缩的特征，我们提高了编解码器的整体效率。

AVC/H.264 中可用于 4×4 块的方向性预测模式图示。预测器将从相邻像素的一像素宽条带中获取的值扩展到以八个方向之一预测的块中，以及用于简单直流预测的平均模式。

运动补偿，一个更古老的想法，也是一种方向性预测的形式，尽管我们很少这样想。它以特定方向移动块，同样是为了在 DCT 之前预测和去除能量。这种块位移是方向性的并经过滤波，并且像方向性帧内预测一样，在位移不是整数个像素时使用精心构建的重采样滤波器。

方向滤波器

如前所述，视频编解码器大量使用滤波来去除块效应和基噪声。虽然滤波器在 2D 平面上工作，但滤波器本身往往是可分离的，也就是说，它们通常是 1D 滤波器，分别以水平和垂直方向分步运行。

方向滤波试图沿除水平和垂直之外的方向运行滤波器。该技术在图像处理中已经很常见，其中降噪和特效滤波器通常是边缘和方向感知的。但是，这些方向滤波器通常基于对方向变换输出的滤波，例如，[有点陈旧的] 我编写的基于 双树复小波 的图像降噪滤波器。

我们对视频编码最感兴趣的方向滤波器需要直接作用于像素，沿着一个方向进行，而不是滤波方向变换的频域输出。一旦您尝试设计这样的滤波器，您很快就会遇到第一个重大设计问题：当您的滤波器抽头位置不再完全落在网格排列的像素上时，如何“跟随”水平和垂直以外的方向？

一种可能性是高质量图像处理中使用的经典方法：变换滤波器内核并根据需要重采样像素空间。甚至有人可能会争辩说，这是唯一“正确”或“完整”的答案。它用于亚像素运动补偿，如果没有至少相当好的重采样，它就无法获得良好的结果，以及在方向性预测中，该预测通常使用快速近似。

也就是说，即使是快速近似在不需要时也很昂贵，因此如果可能，避免重采样步骤是一个值得的目标。速度损失是我们之前在视频编码实践中没有看到方向性滤波的部分原因。

方向变换

方向变换试图在变换本身中修复 DCT 的边缘压缩问题。

实验性方向变换分为两类。有一种变换使用本质上是方向性的基，例如方向小波。这些变换往往是过采样/过完备的，也就是说，它们产生的输出数据多于输入数据——通常多得多。这可能看起来像是倒退；您希望减少数据量，而不是增加它！但是这些变换仍然压缩了能量，并且编码器仍然选择一些小的输出子集进行编码，因此它与通常的无损 DCT 编码没有什么不同。也就是说，过完备变换在内存和计算方面往往比较昂贵，因此，它们尚未在主流视频编码中得到应用。

第二类方向变换采用正则的非方向变换（如 DCT），并通过更改输入或输出对其进行修改。更改可以是重采样、矩阵乘法（可以看作是重采样的特殊形式）或输入数据顺序的调整。

正是最后一个想法最有力量，因为它很快。简单地重新排列数字时，无需进行任何实际的数学运算。

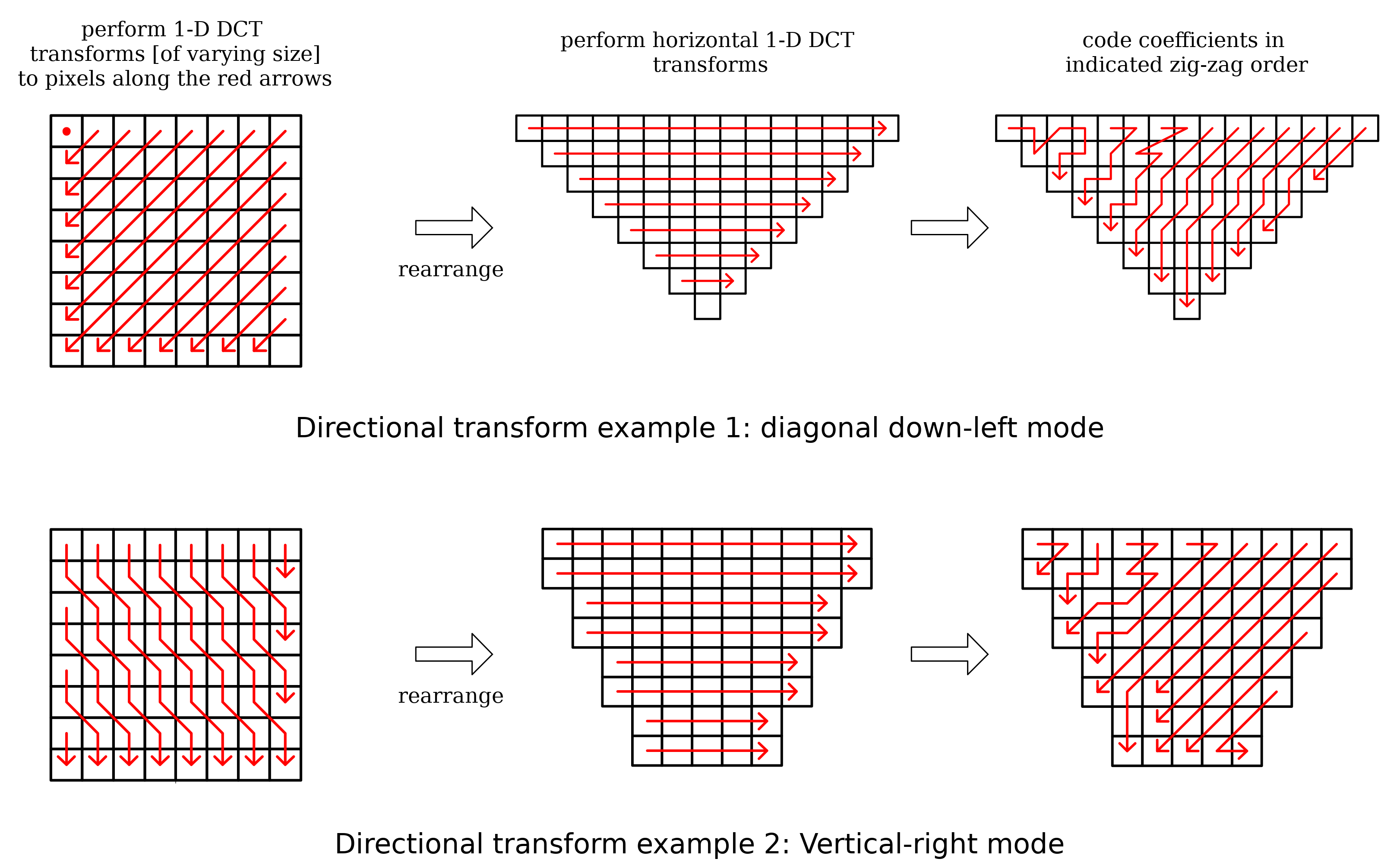
使用像素和系数重排而不是重采样滤波器在不同方向上实现方向变换的两个示例。此示例来自 图像编码中方向变换概述，作者为 Xu、Zeng 和 Wu。

一些实际的复杂情况使得实现变得棘手。重新排列正方形以使对角线边缘变成[主要是]垂直或水平线会导致输入数字的非正方形矩阵。从概念上讲，这不是问题；2D DCT 是可分离的，并且由于我们可以独立运行行和列变换，因此我们可以简单地对每个长度的行和列使用不同大小的 1D DCT，如上图所示。在实践中，这意味着我们需要为每个可能的列长度提供不同的 DCT 分解，并且在意识到这一点后不久，硬件团队就会把你扔出窗外。

还有其他方法来处理重新排列的非正方形，或者提出保持输入正方形或仅对输出进行操作的重采样方案。下面提到的大多数方向变换论文 都关注各种实现此目的的方案。

但方向变换的故事目前主要到此为止。一旦您解决了方向变换的各种复杂情况并部署了一些实用的东西，它们在现代编解码器中却由于一个意想不到的原因而效果不佳：它们与可变块大小的增益相竞争。也就是说，在具有固定块大小的编解码器中，单独添加方向变换可以获得令人印象深刻的效率增益。单独添加可变块大小可以获得更好的增益。将可变块大小和方向变换结合起来不会比单独使用可变块大小获得任何好处。可变块大小已经有效地消除了方向变换利用的相同冗余，至少是我们目前拥有的那些，并且做得更好。

Nathan Egge 和我都在 Daala 研究期间广泛地试验了方向变换。我从输入端和输出端都解决了这个问题，使用稀疏矩阵乘法将对角线边缘的输出转换为垂直/水平排列。Nathan 对主流方向方法进行了重新排列输入的测试。我们得出了相同的结论：额外的复杂性没有带来客观或主观的收益。

方向变换在 Daala（和其他编解码器）中可能失败了，但研究恰好解决了之前提出的一个问题：如何在没有代价高昂的重采样步骤的情况下快速沿边缘进行滤波？答案：不要重采样。通过沿着最近的整像素移动来近似角度。通过字面或概念上重新排列像素来近似变换后的内核。这种方法引入了一些混叠，但它足够好，并且足够快。

方向预测器，第 2 部分：Daala 编年史

Daala在CDEF故事中扮演的角色起源于一次完全不同的尝试：普通的、乏味的、方向性帧内预测。或者至少在Daala编解码器中，这被认为是正常的。

我曾经写过关于Daala的频域帧内预测方案，当时我们才刚刚开始研究它。该方案背后的数学原理是有效的；对此从未有任何疑虑。然而，一个朴素的实现需要一个巨大的矩阵乘法，这对于一个生产环境的编解码器来说代价过于昂贵。我们希望通过稀疏化——消除对预测贡献不大的矩阵元素——可以将计算成本降低到完整乘法的百分之几。

稀疏化并没有像预期的那样奏效。至少在我们实现它的方式下，稀疏化损失了过多的信息，以至于该技术变得不实用。

当然，Daala仍然需要某种形式的帧内预测，而Jean-Marc Valin有一个新的想法：一个独立的预测编解码器，它在空间域工作，并叠加在频域Daala编解码器上。作为一种与Daala编解码器协同工作但没有依赖关系的共生体，它不受Daala的重叠和频域要求的约束。这就是帧内绘制（Intra Paint）的由来。

帧内绘制预测算法应用于悉尼港的照片的示例。视觉输出显然是方向性的，并且很好地遵循了原始图像中的边缘和特征，产生了令人愉悦（尽管有点奇怪）的锐利边缘效果。

帧内绘制的工作方式也很新颖；它只沿着块的边缘编码一维向量，然后沿着选定的方向扫过图案。这就像沿着一条线喷射彩色油漆点，然后沿不同的方向将油漆扫过开放区域。

帧内绘制很有前景，并且自身产生了一些令人惊叹的漂亮结果，但同样效率不够高，无法用作标准的帧内预测器。它获得的比特数 simply didn't gain back enough bits over the bits it had to use to code its own information.

原始悉尼港照片与帧内绘制结果之间的差异。尽管帧内绘制的视觉输出令人愉悦，但我们看到它并不是一个客观上超级精确的预测器。原始照片和帧内绘制结果之间的差异相当大，即使是在它看起来复制得很好的许多边缘处也是如此。

帧内绘制的“失败”再次播下了不同想法的种子；尽管绘制在客观上可能不够精确，无法用作预测器，但其大部分输出在主观上看起来都相当不错。也许绘制技术可以作为一种后处理滤波器来提高主观视觉质量？帧内绘制很好地遵循强边缘，因此可以潜在地用于消除往往在最强边缘处最强的基噪声。这就是最初的Daala绘制去环滤波器的想法，最终导致了CDEF本身。

关于方向预测，还有一个值得一提的有趣话题，尽管它目前也是视频编码的死胡同。David Schleef实现了一个有趣的边缘/方向感知重采样滤波器，称为边缘导向插值（EDI）。其他编解码器（如VPx系列和一段时间内的AV1）已经尝试使用下采样参考帧，以在下采样状态传输参考帧以节省编码比特，然后对参考帧进行上采样以在全分辨率下使用。我们希望EDI提供的改进后的上采样/插值可以使该技术变得有用。我们还希望将EDI用作运动补偿的改进型亚像素插值滤波器。遗憾的是，这些想法仍然是一个未实现的梦想。

弥合差距，融合线索

至此，我已经描述了接近CDEF所需的所有主要背景，但在时间顺序上，这个故事还涉及到在沙漠中的一些进一步徘徊。帧内绘制产生了最初的Daala绘制去环滤波器，该滤波器重新实现了帧内绘制算法，以作为后置滤波器执行去环。绘制去环证明对于生产环境来说速度太慢了。

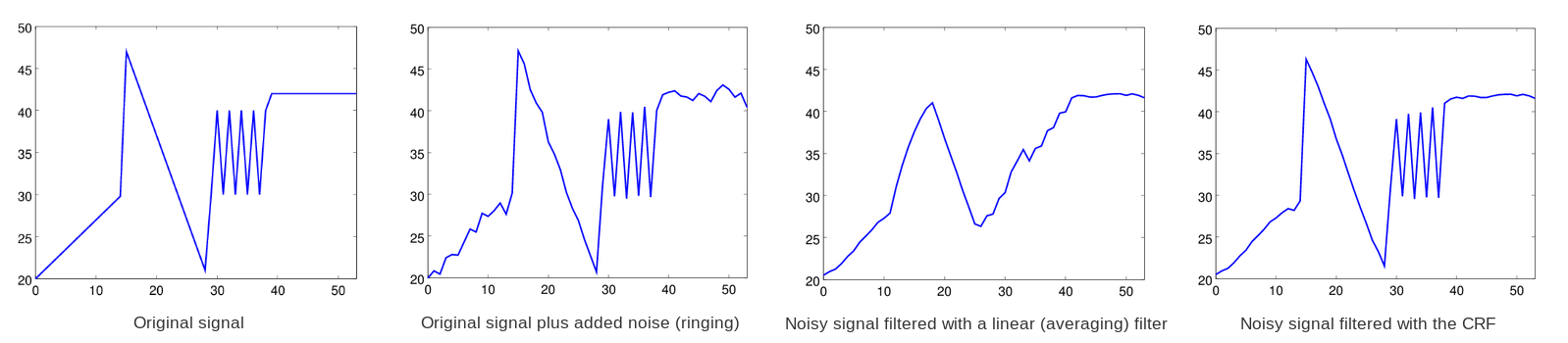
因此，我们总结了从帧内绘制中学到的经验教训，并最终放弃了这条实验路线。Daala在一段时间内引入了Thor的CLPF，然后Jean-Marc基于帧内绘制边缘方向搜索（速度快且效果好）和条件替换滤波器（CRF）构建了第二个更快得多的Daala去环滤波器。CRF在某种程度上受到中值滤波器的启发，产生的结果类似于双边滤波器，但本质上具有高度矢量化特性，因此速度更快。

7抽头线性滤波器与约束替换滤波器应用于噪声一维信号的演示，其中噪声旨在模拟量化对原始信号的影响。

最终的Daala去环滤波器使用了两个一维CRF滤波器，一个沿边缘方向运行的7抽头滤波器，以及一个较弱的横向运行的5抽头滤波器。这两个滤波器仅对整个像素进行操作，不执行重采样。在这一点上，Daala去环滤波器开始看起来非常像我们现在所知的CDEF。

我们最近将Daala提交给AOM作为输入编解码器，这个中间滤波器成为了AV1的daala_dering实验。思科也提交了他们自己的去环滤波器，即来自Thor编解码器的约束低通滤波器（CLPF）。在一段时间内，这两个去环滤波器在AV1实验代码库中并存，可以单独启用，甚至可以一起运行。这导致双方都注意到它们操作中的有用协同作用，以及滤波器各个阶段的其他相似之处。

因此，我们最终得到了CDEF：将思科的CLPF滤波器和Daala去环滤波器的第二个版本合并成一个单一的、高性能的、方向感知的去环滤波器。

现代CDEF

CDEF滤波器很简单，并且与我们之前的滤波器有着很深的相似之处。它由三个部分（方向搜索、约束替换/低通滤波器和整数像素抽头放置）构成，我们之前已经使用过这些部分。鉴于到目前为止的冗长背景介绍，你可能会看着完成的CDEF并想，“就这些？剩下的部分在哪里？”CDEF是一个例子，它说明了通过精确地调整滤波器的细节而不是简单地使其变得越来越复杂而获得的收益。简单有效是一个好的目标。

方向搜索

CDEF在特定方向上运行，因此有必要确定该方向。使用的搜索算法与帧内绘制和绘制去环相同，并且有八个可能的方向。

当前CDEF滤波器的八个可能的滤波方向。每个方向块中的编号线对应于方向搜索中的“k”参数。

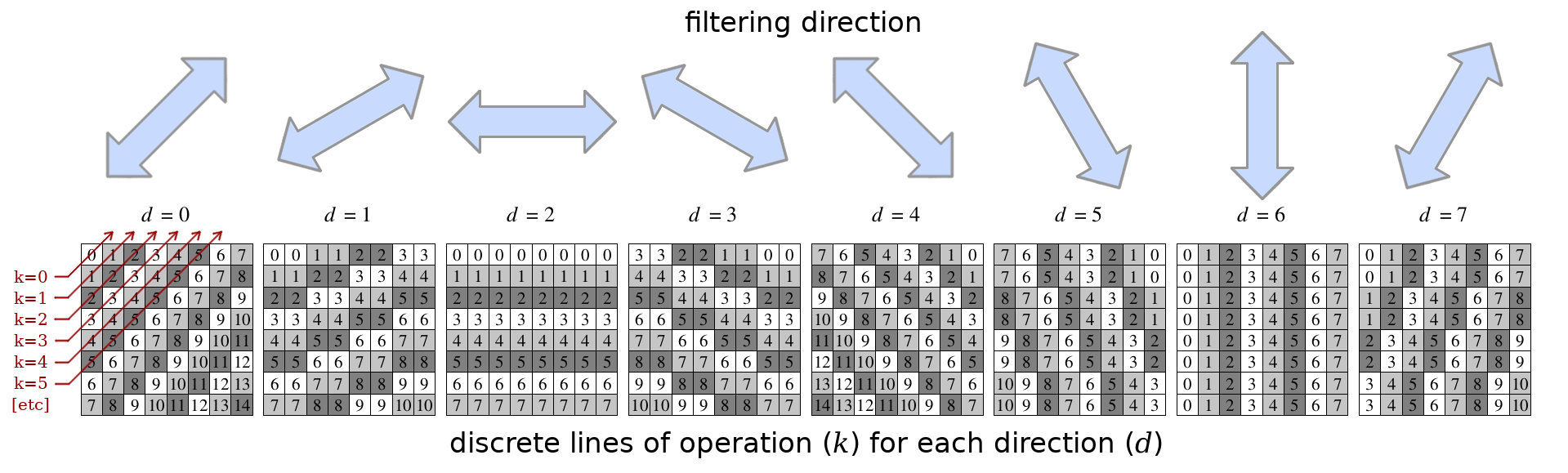
我们通过为每个方向创建输入块的“方向”变体来确定滤波方向，其中所选方向上的所有像素都强制具有相同的值。然后我们选择结果最接近原始块的方向。也就是说，对于每个方向d，我们首先找到每行像素的平均值k，然后沿着每行计算给定像素值与其像素行平均值之间的平方误差之和。

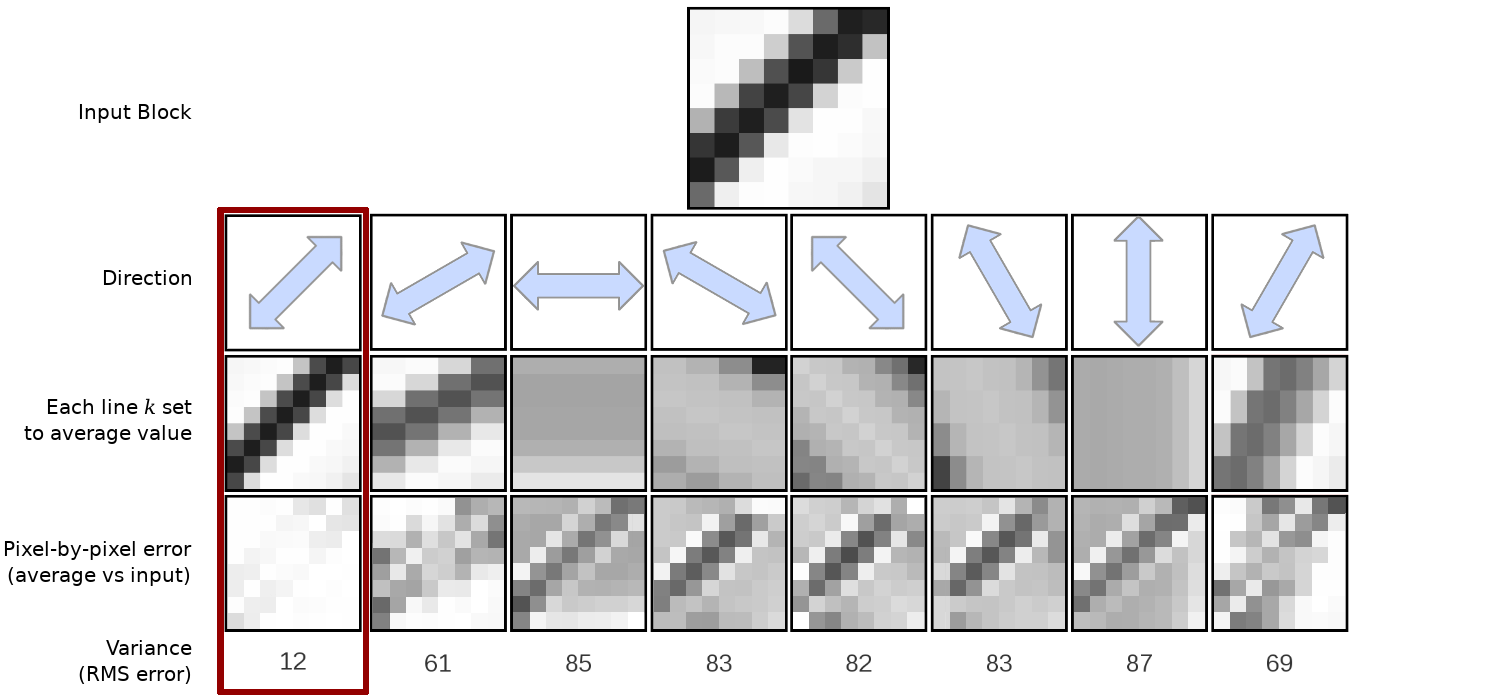
选择最匹配输入块的方向的示例过程。d首先，我们确定每个方向的每行操作的平均像素值。k如上所示，通过将给定行的每个像素k设置为该平均值来进行说明。然后，我们通过从平均值中减去输入值来对给定方向逐像素计算误差。误差/方差最小的方向被选为最佳方向。

这给了我们总的平方误差，并且总的平方误差最低的方向是我们选择的方向。尽管上面的图示示例也这样做，但没有理由将平方误差转换为方差；每个方向都考虑相同数量的像素，因此两者都会选择相同的答案。节省额外的除法！

这是计算方向误差的直观、冗长的方式。我们可以将机械过程简化为以下等式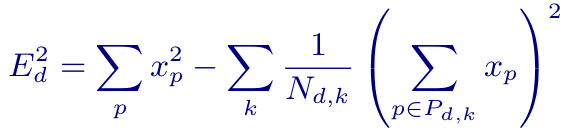：在这个等式中，E是误差，p是一个像素，xp是像素的值，k是上面方向图中的编号行之一，并且Nd,k是行（方向k中像素的数量）的基数。d这个等式在实践中可以简化；例如，第一个项对于每个给定的d都是相同的。最终，AV1中CDEF的实现目前每个像素需要5.875次加法和1.9375次乘法，并且可以深度矢量化，导致总成本低于8×8 DCT。

滤波器抽头

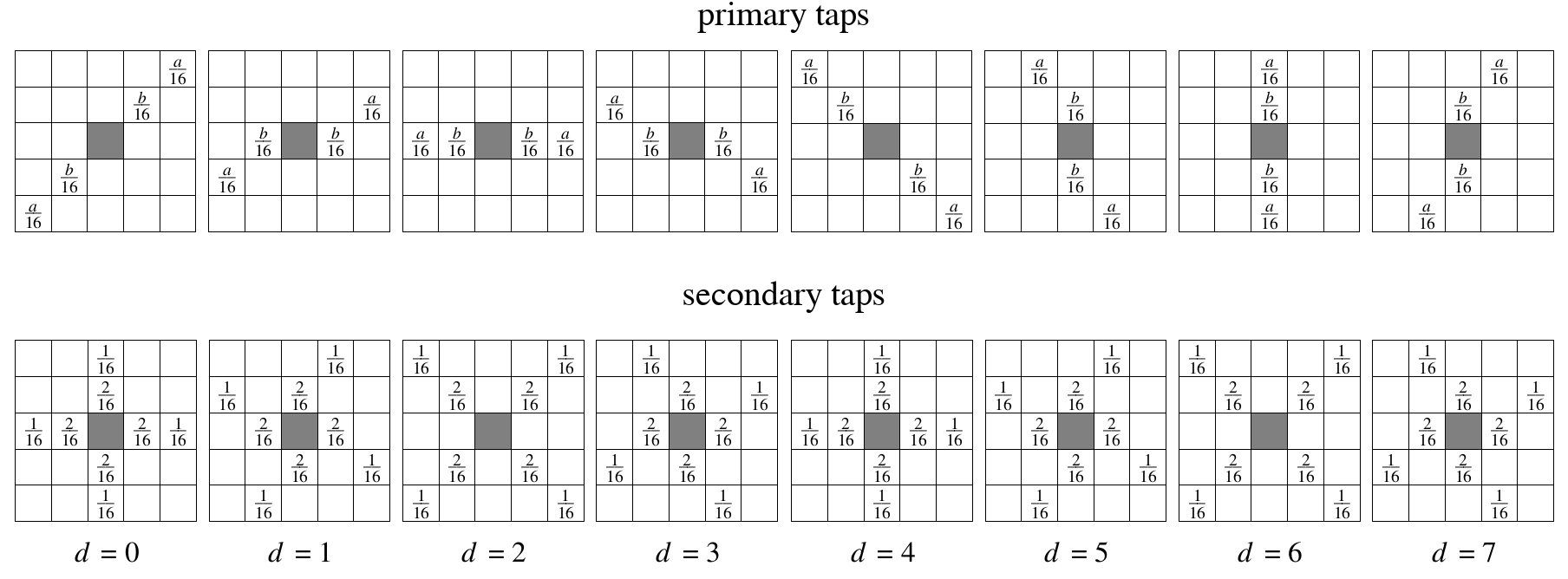
CDEF滤波器逐像素地处理整个块。方向d选择要使用的特定方向滤波器，每个滤波器都由一组滤波器抽头（即输入像素位置）和抽头权重组成。

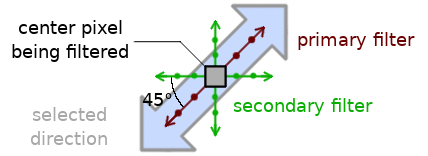
CDEF在概念上用两个一维滤波器构建方向滤波器。主滤波器沿选定的方向运行，就像在Daala去环滤波器中一样。次滤波器以45°角交叉模式运行两次，就像在Thor的CLPF中一样。

主滤波器和次滤波器方向性相对于所选方向的示意图d。主滤波器沿着所选滤波方向运行，次滤波器以45°角横跨所选方向运行。块中的每个像素都以相同的方式进行滤波。

滤波器以通常将理想抽头位置放置在像素之间的角度运行。我们不是进行重采样，而是选择最近的精确像素位置，并注意构建对称滤波器核。

滤波器中的每个抽头也都有一个固定权重。滤波过程获取每个抽头的输入值，应用约束函数，将结果乘以抽头的固定权重，然后将此输出值添加到正在滤波的像素中。

主滤波器和次滤波器抽头位置以及根据滤波方向固定的权重（w）。对于主抽头和偶数强度，a = 2且b = 4，而对于奇数强度，a = 3且b = 3。滤波后的像素以灰色显示。

在实践中，主滤波器和次滤波器不是分别运行，而是组合成一个单一的滤波器核，并在一步中运行。

约束函数

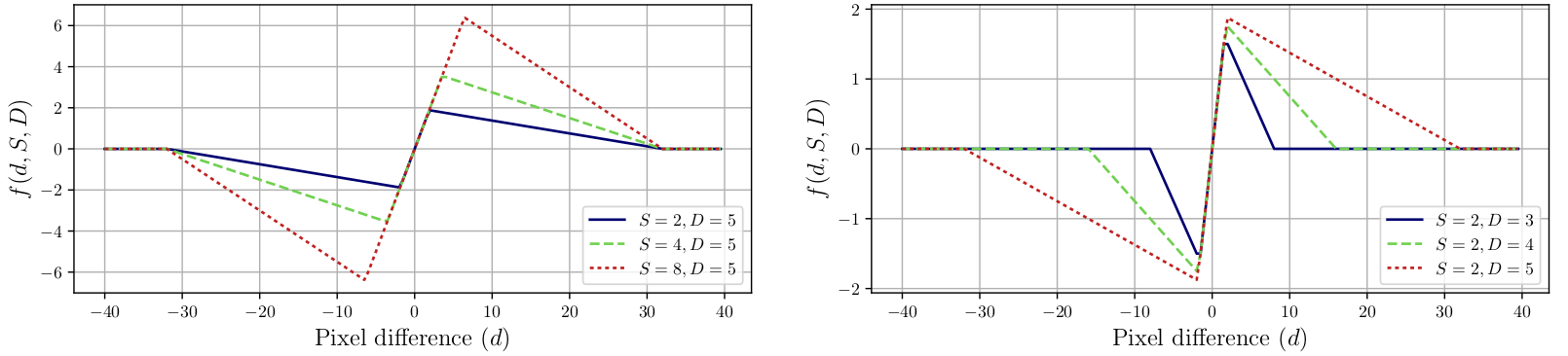
CDEF使用约束低通滤波器，其中每个滤波器抽头的值首先通过一个约束函数进行处理，该函数由抽头值与正在滤波的像素之间的差异参数化d、滤波器强度S和滤波器阻尼参数D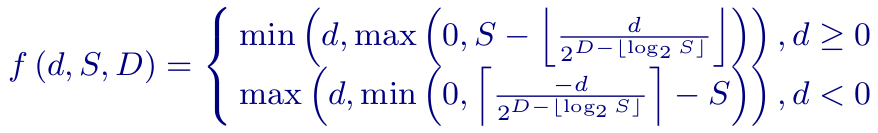：约束函数旨在弱化或完全拒绝考虑与正在滤波的像素差异过大的像素。在一定范围内（由强度参数S设置）从中心像素值内的抽头值差异被完全考虑。落在强度和阻尼参数之间的值差异被弱化。最后，超过阻尼参数的抽头值差异被忽略。

约束函数的示意图。在两个图中，正在考虑的中心像素与抽头像素之间的差异（d）位于x轴上。约束函数的输出值位于y轴上。左图说明了改变强度（S）参数的影响。右图展示了改变阻尼（D).

的影响。(p)和(s)标记主和次抽头组的值。

关于舍入和裁剪，还有一些额外的实现细节，理解这些细节对于理解来说并不必要；如果你打算实现CDEF，当然可以在完整的CDEF论文中找到它们。

结果

CDEF旨在消除或减少图像中硬边缘周围的基噪声和环状伪影，而不会模糊或损坏边缘。在目前AV1中的使用中，效果微妙但一致。将来可能可以更大幅度地依赖CDEF。

图像水果编码中环状伪影/基噪声减少的示例。第一个内嵌特写显示了未经CDEF处理的区域，第二个内嵌特写显示了CDEF处理后的同一区域。

任何增强滤波器的定量值必须通过主观测试来确定。更好的客观指标数字也不会令人惊讶，但激励CDEF的视觉改进大多超出了PSNR或SSIM等原始客观测试工具的评估能力。

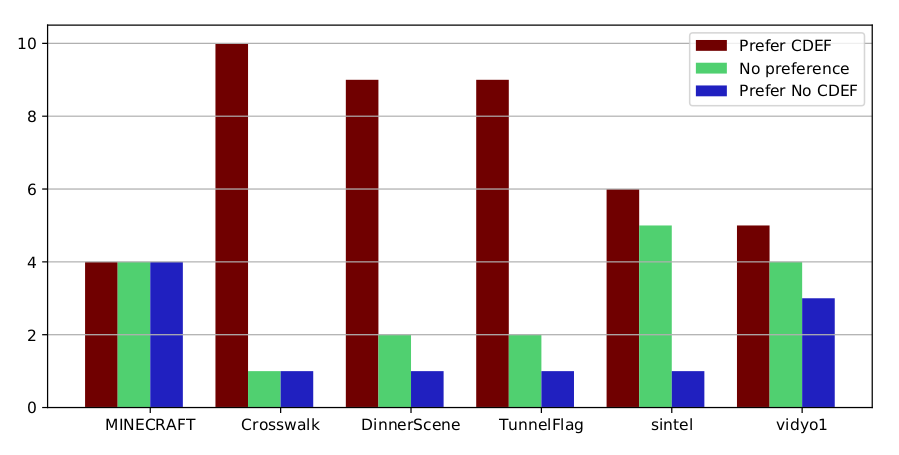
因此，我们进行了多轮主观测试，首先是在CDEF开发期间（当时Daala去环和Thor CLPF在技术上仍然是竞争对手），然后是对合并的CDEF滤波器进行更广泛的测试。由于CDEF是一个前几代编解码器中完全不存在的新滤波器，因此测试主要包括启用CDEF的AV1与禁用CDEF的AV1。

高延迟配置下CDEF与无CDEF的主观A-B比较结果（含平局）。

主观结果显示，在6个片段中有3个片段的改进具有统计学意义（p<.05）。这通常对应于5-10%的编码效率提升，对于添加到一个已经成熟的编解码器中的单个工具来说，这是一个相当大的收益。

正如预期的那样，客观测试显示出大约 1% 的适度改进，但是客观测试主要仅在与主观结果一致的情况下才有用。主观测试是黄金标准，主观结果是明确的。

测试还表明，当使用较少的编解码器“工具”（如方向变换）进行编码时，CDEF 的性能更好；CDEF 在 AV1 中与其他更复杂的技术竞争编码增益。由于 CDEF 简单、小巧且快速，因此它可以提供未来降低 AV1 编码器复杂性的方法。就解码器复杂性而言，CDEF 占 AV1 解码器的 3% 到 10%，具体取决于配置。

其他资源